List of exercises

Summary

JupyterLab and notebook interface:

Tools for writing, testing and debugging code

A first computational notebook:

Notebooks and version control:

plain-git-diff

Sharing notebooks:

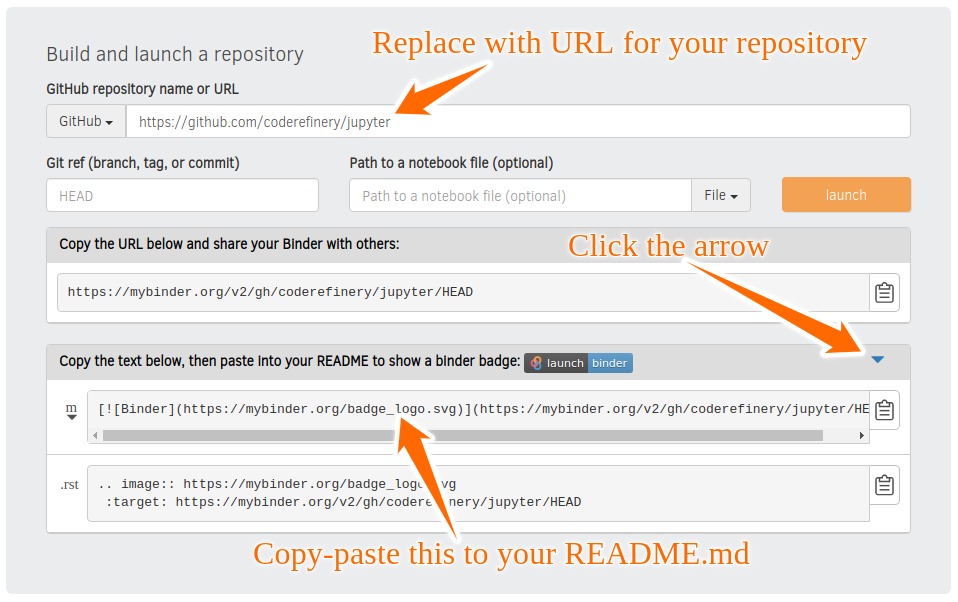
Examples of Jupyter features:

Full list

This is a list of all exercises and solutions in this lesson, mainly as a reference for helpers and instructors. This list is automatically generated from all of the other pages in the lesson. Any single teaching event will probably cover only a subset of these, depending on their interests.

A first computational notebook

In first-notebook.md:

Exercise/demonstration: Calculating pi using Monte Carlo methods

This can be either done as a 20 minute exercise or as a type-along demo.

Each numbered item will be a new cell. Press SHIFT+ENTER to run a cell and create a new cell below. With the cell selected, press ESCAPE to go into command mode. Use shortcuts M and Y to change cells to markdown and code, respectively.

Create a new notebook, name it, and add a heading (markdown cell).
```
# Calculating pi using Monte Carlo methods
```

Document the relevant formulas in a new cell (markdown cell):

## Relevant formulas

- square area: $s = (2 r)^2$
- circle area: $c = \pi r^2$
- $c/s = (\pi r^2) / (4 r^2) = \pi / 4$
- $\pi = 4 * c/s$

Add an image to explain the concept (markdown cell):

## Image to visualize the concept

![Darts](https://raw.githubusercontent.com/coderefinery/jupyter/main/example/darts.svg)

Import two modules that we will need (code cell):

# importing modules that we will need

import random
import matplotlib.pyplot as plt

Initialize the number of points (code cell):

# initializing the number of "throws"

num_points = 1000

“Throw darts” (code cell):

# here we "throw darts" and count the number of hits

points = []
hits = 0
for _ in range(num_points):
    x, y = random.random(), random.random()
    if x*x + y*y < 1.0:
        hits += 1
        points.append((x, y, "red"))
    else:
        points.append((x, y, "blue"))

Plot results (code cell):

# unzip points into 3 lists
x, y, colors = zip(*points)

# define figure dimensions
fig, ax = plt.subplots()
fig.set_size_inches(6.0, 6.0)

# plot results
ax.scatter(x, y, c=colors)

Compute the estimate for pi (code cell):

# compute and print the estimate

fraction = hits / num_points
4 * fraction

Notebooks and version control

In version-control.md:

Instructor demonstrates a plain git diff

To understand the problem, the instructor first shows the example notebook and then the source code in JSON format.
Then we introduce a simple change to the example notebook, for instance changing colors (change “red” and “blue” to something else) and also changing dimensions in fig.set_size_inches(6.0, 6.0).
Run all cells.
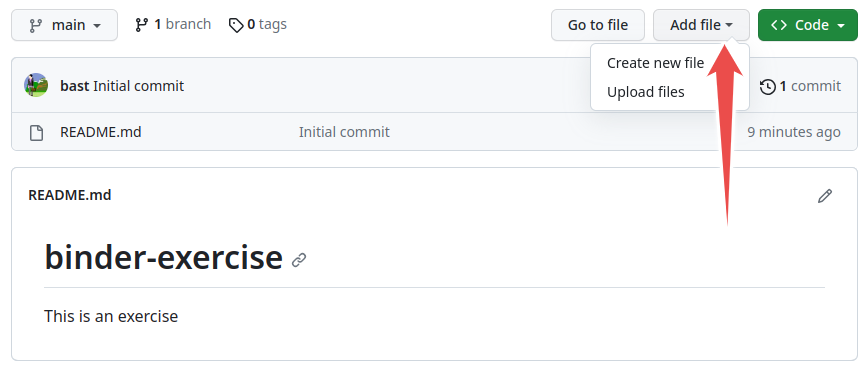
We save the change (save icon) and in the JupyterLab terminal try a “normal” git diff and see that this is not very useful. Discuss why.

Shell commands, magics and widgets

In extra-features.md:

A few useful magic commands

Using the computing-pi notebook, practice using a few magic commands. Remember that cell magics need to be on the first line of the cell.

In the cell with the for-loop over num_points (throwing darts), add the %%timeit cell magic and run the cell.
In the same cell, try instead the %%prun cell profiling magic.
Try introducing a bug in the code (e.g., use an incorrect variable name: points.append((x, y2, True)))
- run the cell
- after the exception occurs, run the %debug magic in a new cell to enter an interactive debugger
- type h for a help menu, and help <keyword> for help on keyword
- type p x to print the value of x
- exit the debugger by typing q
Have a look at the output of %lsmagic, and use a question mark and double question mark to see help for a magic command that raises your interest.

In extra-features.md:

Playing around with a widget

Widgets can be used to interactively explore or analyze data.

We return to the pi approximation example and create a new cell where we reuse code that we have written earlier but this time we place the code into functions. This “hides” details and allows us to reuse the functions later or in other notebooks:

import random
from ipywidgets import interact, widgets

%matplotlib inline
from matplotlib import pyplot


def throw_darts(num_points):
    points = []
    hits = 0
    for _ in range(num_points):
        x, y = random.random(), random.random()
        if x*x + y*y < 1.0:
            hits += 1
            points.append((x, y, True))
        else:
            points.append((x, y, False))
    fraction = hits / num_points
    pi = 4 * fraction
    return pi, points


def create_plot(points):
    x, y, colors = zip(*points)
    pyplot.scatter(x, y, c=colors)


def experiment(num_points):
    pi, points = throw_darts(num_points)
    create_plot(points)
    print("approximation:", pi)

Try to call the experiment function with e.g. num_points set to 2000.
Add a cell where we will make it possible to vary the number of points interactively:
```
interact(experiment, num_points=widgets.IntSlider(min=100, max=10000, step=100, value=1000))
```
If you run into Error displaying widget: model not found, you may need to refresh the page.
Drag the slider back and forth and observe the results.
Can you think of other interesting uses of widgets?

Examples of Jupyter features

In examples.md:

Widgets for interactive data fitting

Widgets are fun, but they can also be useful. Here’s an example showing how you can fit noisy data interactively.

Execute the cell below. It fits a 5th order polynomial to a gaussian function with some random noise
Use the @interact decorator around the last two code lines such that you can visualize fits with polynomial orders n ranging from, say, 3 to 30:

import numpy as np

import matplotlib.pyplot as plt
%matplotlib inline

def gaussian(x, a, b, c):
    return a * np.exp(-b * (x-c)**2)

def noisy_gaussian():
    # gaussian array y in interval -5 <= x <= 5
    nx = 100
    x = np.linspace(-5.0, 5.0, nx)
    y = gaussian(x, a=2.0, b=0.5, c=1.5)
    noise = np.random.normal(0.0, 0.2, nx)
    y += noise
    return x, y

def fit(x, y, n):
    pfit = np.polyfit(x, y, n)
    yfit = np.polyval(pfit, x)
    return yfit

def plot(x, y, yfit):
    plt.plot(x, y, "r", label="Data")
    plt.plot(x, yfit, "b", label="Fit")
    plt.legend()
    plt.ylim(-0.5, 2.5)
    plt.show()

x, y = noisy_gaussian()
yfit = fit(x, y, n=5)  # fit a 5th order polynomial to it
plot(x, y, yfit)

Solution

import numpy as np

from ipywidgets import interact

import matplotlib.pyplot as plt
%matplotlib inline

def gaussian(x, a, b, c):
    return a * np.exp(-b * (x-c)**2)

def noisy_gaussian():
    # gaussian array y in interval -5 <= x <= 5
    nx = 100
    x = np.linspace(-5.0, 5.0, nx)
    y = gaussian(x, a=2.0, b=0.5, c=1.5)
    noise = np.random.normal(0.0, 0.2, nx)
    y += noise
    return x, y

def fit(x, y, n):
    pfit = np.polyfit(x, y, n)
    yfit = np.polyval(pfit, x)
    return yfit

def plot(x, y, yfit):
    plt.plot(x, y, "r", label="Data")
    plt.plot(x, yfit, "b", label="Fit")
    plt.legend()
    plt.ylim(-0.5, 2.5)
    plt.show()

x, y = noisy_gaussian()

@interact
def slider(n=(3, 30)):
    yfit = fit(x, y, n)
    plot(x, y, yfit)

In examples.md:

Cell profiling

This exercise is about cell profiling, but you will get practice in working with magics and cells.

Copy-paste the following code into a cell:

import numpy as np
import matplotlib.pyplot as plt

def step():
    import random
    return 1. if random.random() > .5 else -1.

def walk(n):
    x = np.zeros(n)
    dx = 1. / n
    for i in range(n - 1):
        x_new = x[i] + dx * step()
        if x_new > 5e-3:
            x[i + 1] = 0.
        else:
            x[i + 1] = x_new
    return x

n = 100000
x = walk(n)

Split up the functions over 4 cells (either via Edit menu or keyboard shortcut Ctrl-Shift-minus).
Plot the random walk trajectory using plt.plot(x).
Time the execution of walk() with a line magic.
Run the prun cell profiler.
Can you spot a little mistake which is slowing down the code?
In the next exercise you will install a line profiler which will more easily expose the performance mistake.

Solution

Split the code over multiple cells (e.g. using Ctrl-Shift-minus)

import numpy as np

def step():
    import random
    return 1. if random.random() > .5 else -1.

def walk(n):
    x = np.zeros(n)
    dx = 1. / n
    for i in range(n - 1):
        x_new = x[i] + dx * step()
        if x_new > 5e-3:
            x[i + 1] = 0.
        else:
            x[i + 1] = x_new
    return x

Initialize n and call walk():

n = 100000
x = walk(n)

Plot the random walk

import matplotlib.pyplot as plt
plt.plot(x);

Time the execution using the %timeit line magic, and capture the output:

t1 = %timeit -o walk(n)

Best result

t1.best

Run with the %%prun cell profiler

%%prun
walk(n)

In examples.md:

Installing a magic command for line profiling

Magics can be installed using pip and loaded like plugins using the %load_ext magic. You will now install a line-profiler to get more detailed profile, and hopefully find insight to speed up the code from the previous exercise.

If you haven’t solved the previous exercise, copy paste the following code into a cell and run it:

import numpy as np
import matplotlib.pyplot as plt

def step():
    import random
    return 1. if random.random() > .5 else -1.

def walk(n):
    x = np.zeros(n)
    dx = 1. / n
    for i in range(n - 1):
        x_new = x[i] + dx * step()
        if x_new > 5e-3:
            x[i + 1] = 0.
        else:
            x[i + 1] = x_new
    return x

n = 100000
x = walk(n)

Then install the line profiler using !pip install line_profiler.
Next load it using %load_ext line_profiler.
Have a look at the new magic command that has been enabled with %lprun?
In a new cell, run the line profiler on the walk and step functions in the way described on the help page.
Inspect the output. Can you more easily see the mistake now?

Solution

Copy-paste the code into a cell

Install the line profiler

!pip install line_profiler

Load the IPython extension

%load_ext line_profiler

See help:

%lprun?

Use the line profiler on the walk function:

%lprun -f walk walk(10000)

Aha, most time is spent on the line calling the step() function. Run line profiler on step:

%lprun -f step walk(10000)

...
     8                                           def step():
     9      9999       7488.0      0.7     52.3      import random
    10      9999       6840.0      0.7     47.7      return 1. if random.random()
...

Aha! Lot’s of time is spent on importing the random module inside the step function which is called thousands of times. Move the import statement to outside the function!

In examples.md:

Data analysis with pandas dataframes

Data science and data analysis are key use cases of Jupyter. In this exercise you will familiarize yourself with dataframes and various inbuilt analysis methods in the high-level pandas data exploration library. A dataset containing information on Nobel prizes will be viewed with the file browser.

Start by navigating in the File Browser to the data/ subfolder, and double-click on the nobels.csv dataset. This will open JupyterLab’s inbuilt data browser.
Have a look at the data, column names, etc.
In a your own notebook, import the pandas module and load the dataset into a dataframe:

import pandas as pd
nobel = pd.read_csv("data/nobels.csv")

The “share” column of the dataframe contains the number of Nobel recipients that shared the prize. Have a look at the statistics of this column using

nobel["share"].describe()

The describe() method is smart about data types. Try this:

nobel["bornCountryCode"].describe()

- What country has received the largest number of Nobel prizes, and how many?
- How many countries are represented in the dataset?

Now analyze the age of prize recipients. You first need to convert the “born” column to datetime format:

nobel["born"] = pd.to_datetime(nobel["born"],
                               errors ='coerce')

Next subtract the birth date from the year of receiving the prize and insert it into a new column “age”:

nobel["age"] = nobel["year"] - nobel["born"].dt.year

Now print the “surname” and “age” of first 10 entries using the head() method.

Now plot results in two different ways:

nobel["age"].plot.hist(bins=[20,30,40,50,60,70,80,90,100], alpha=0.6);
nobel.boxplot(column="age", by="category")

Which Nobel laureates have been Swedish? See if you can use the nobel.loc[CONDITION] statement to extract the relevant rows from the nobel dataframe using the appropriate condition.
Finally, try the powerful groupby() method to analyze the number of Nobel prizes per country, and visualize it with the high-level seaborn plotting library.

First add a column “number” to the nobel dataframe containing 1’s (to enable the counting below).
Then extract any 4 countries (replace below) and create a subset of the dataframe:

countries = np.array([COUNTRY1, COUNTRY2, COUNTRY3, COUNTRY4])
nobel2 = nobel.loc[nobel['bornCountry'].isin(countries)]

Next use groupby() and sum(), and inspect the resulting dataframe:

nobels_by_country = nobel2.groupby(['bornCountry',"category"], sort=True).sum()

Next use the pivot_table method to reshape the dataframe to a spreadsheet-like structure, and display the result:

table = nobel2.pivot_table(values="number", index="bornCountry", columns="category", aggfunc=np.sum)

Finally visualize using a heatmap:

import seaborn as sns
sns.heatmap(table,linewidths=.5);

Have a look at the help page for sns.heatmap and see if you can find an input parameter which annotates each cell in the plot with the count number.

Solution

import numpy as np
import pandas as pd
nobel = pd.read_csv("data/nobels.csv")

nobel["share"].describe()

nobel["bornCountryCode"].describe()

USA has received 275 prizes.
76 countries have received at least one prize.

nobel["born"] = pd.to_datetime(nobel["born"], errors ='coerce')

Add column

nobel["age"] = nobel["year"] - nobel["born"].dt.year

Print surname and age

nobel[["surname","age"]].head(10)

nobel["age"].plot.hist(bins=[20,30,40,50,60,70,80,90,100],alpha=0.6);

nobel.boxplot(column="age", by="category")

Which Nobel laureates have been Swedish?

nobel.loc[nobel["bornCountry"] == "Sweden"]

Finally, try the powerful groupby() method. Add extra column with number of Nobel prizes per row (needed for statistics)

nobel["number"] = 1.0

Pick a few countries to analyze further

countries = np.array(["Sweden", "United Kingdom", "France", "Denmark"])
nobel2 = nobel.loc[nobel['bornCountry'].isin(countries)]

table = nobel2.pivot_table(values="number", index="bornCountry",
                           columns="category", aggfunc=np.sum)
table

import seaborn as sns
sns.heatmap(table,linewidths=.5, annot=True);

In examples.md:

Defining your own custom magic command

It is possible to create new magic commands using the @register_cell_magic decorator from the IPython.core library. Here you will create a cell magic command that compiles C++ code and executes it. This exercise requires that you have the GNU g++ compiler installed on your computer.

This example has been adapted from the IPython Minibook, by Cyrille Rossant, Packt Publishing, 2015.

First import register_cell_magic

from IPython.core.magic import register_cell_magic

Next copy-paste the following code into a cell, and execute it to register the new cell magic command:

@register_cell_magic
def cpp(line, cell):
    """Compile, execute C++ code, and return the standard output."""

    # We first retrieve the current IPython interpreter instance.
    ip = get_ipython()
    # We define the source and executable filenames.
    source_filename = '_temp.cpp'
    program_filename = '_temp'
    # We write the code to the C++ file.
    with open(source_filename, 'w') as f:
        f.write(cell)
    # We compile the C++ code into an executable.
    compile = ip.getoutput("g++ {0:s} -o {1:s}".format(
        source_filename, program_filename))
    # We execute the executable and return the output.
    output = ip.getoutput('./{0:s}'.format(program_filename))
    print('\n'.join(output))

You can now start using the magic using %%cpp.

Write some C++ code into a cell and try executing it.
To be able to use the magic in another notebook, you need to add the following function at the end and then write the cell to a file in your PYTHONPATH. If the file is called cpp_ext.py, you can then load it by %load_ext cpp_ext.

def load_ipython_extension(ipython):
    ipython.register_magic_function(cpp,'cell')

Solution

from IPython.core.magic import register_cell_magic

Add load_ipython_extension function, and write cell to file called cpp_ext.py:

%%writefile cpp_ext.py
def cpp(line, cell):
    """Compile, execute C++ code, and return the standard output."""

    # We first retrieve the current IPython interpreter instance.
    ip = get_ipython()
    # We define the source and executable filenames.
    source_filename = '_temp.cpp'
    program_filename = '_temp'
    # We write the code to the C++ file.
    with open(source_filename, 'w') as f:
        f.write(cell)
    # We compile the C++ code into an executable.
    compile = ip.getoutput("g++ {0:s} -o {1:s}".format(
        source_filename, program_filename))
    # We execute the executable and return the output.
    output = ip.getoutput('./{0:s}'.format(program_filename))
    print('\n'.join(output))

def load_ipython_extension(ipython):
    ipython.register_magic_function(cpp,'cell')

Load extension:

%load_ext cpp_ext

Get help on the cpp magic:

%%cpp?

Hello World program in C++

%%cpp
#include <iostream>
using namespace std;

int main()
{
    cout << "Hello, World!";
    return 0;
}

In examples.md:

Parallel Python with ipyparallel

Traditionally, Python is considered to not support parallel programming very well (see “GIL”), and “proper” parallel programming should be left to “heavy-duty” languages like Fortran or C/C++ where OpenMP and MPI can be utilised.

However, IPython now supports many different styles of parallelism which can be useful to researchers. In particular, ipyparallel enables all types of parallel applications to be developed, executed, debugged, and monitored interactively. Possible use cases of ipyparallel include:

Quickly parallelize algorithms that are embarrassingly parallel using a number of simple approaches.
Run a set of tasks on a set of CPUs using dynamic load balancing.
Develop, test and debug new parallel algorithms (that may use MPI) interactively.
Analyze and visualize large datasets (that could be remote and/or distributed) interactively using IPython

This exercise is just to get started, for a thorough treatment see the official documentation and this detailed tutorial.

First install ipyparallel using conda or pip. Open a terminal window inside JupyterLab and do the installation.
After installing ipyparallel, you need to start an “IPython cluster”. Do this in the terminal with ipcluster start.
Then import ipyparallel in your notebook, initialize a Client instance, and create DirectView object for direct execution on the engines:

import ipyparallel as ipp
client = ipp.Client()
print("Number of ipyparallel engines:", len(client.ids))
dview = client[:]

You have now started the parallel engines. To run something simple on each one of them, try the apply_sync() method:

dview.apply_sync(lambda : "Hello, World")

A serial evaluation of squares of integers can be seen in the code snippet below.

serial_result = list(map(lambda x:x**2, range(30)))

Convert this to a parallel calculation on the engines using the map_sync() method of the DirectView instance. Time both serial and parallel versions using %%timeit -n 1.

You will now parallelize the evaluation of pi using a Monte Carlo method. First load modules, and export the random module to the engines:

from random import random
from math import pi
dview['random'] = random

Then execute the following code in a cell. The function mcpi is a Monte Carlo method to calculate $\pi$. Time the execution of this function using %timeit -n 1 and a sample size of 10 million (int(1e7)).

def mcpi(nsamples):
    s = 0
    for i in range(nsamples):
        x = random()
        y = random()
        if x*x + y*y <= 1:
            s+=1
    return 4.*s/nsamples

Now take the incomplete function below which takes a DirectView object and a number of samples, divides the number of samples between the engines, and calls mcpi() with a subset of the samples on each engine. Complete the function (by replacing the ____ fields), call it with $10^7$ samples, time it and compare with the serial call to mcpi().

def multi_mcpi(dview, nsamples):
    # get total number target engines
    p = len(____.targets)
    if nsamples % p:
        # ensure even divisibility
        nsamples += p - (nsamples%p)

    subsamples = ____//p

    ar = view.apply(mcpi, ____)
    return sum(ar)/____

Final note: While parallelizing Python code is often worth it, there are other ways to get higher performance out of Python code. In particular, fast numerical packages like Numpy should be used, and significant speedup can be obtained with just-in-time compilation with Numba and/or C-extensions from Cython.

Solution

Open terminal, run ipcluster start and wait a few seconds for the engines to start. Import module, create client and DirectView object:

import ipyparallel as ipp
client = ipp.Client()
dview = client[:]
dview

<DirectView [0, 1, 2, 3]>

Time the serial evaluation of the squaring lambda function:

%%timeit -n 1
serial_result = list(map(lambda x:x**2, range(30)))

Use the map_sync method of the DirectView instance:

%%timeit -n 1
parallel_result = list(dview.map_sync(lambda x:x**2, range(30)))

There probably won’t be any speedup due to the communication overhead.

Focus instead on computing pi. Import modules, export random module to engines:

from random import random
from math import pi
dview['random'] = random

def mcpi(nsamples):
    s = 0
    for i in range(nsamples):
        x = random()
        y = random()
        if x*x + y*y <= 1:
            s+=1
    return 4.*s/nsamples

%%timeit -n 1
mcpi(int(1e7))

3.05 s ± 97.1 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

Function for splitting up the samples and dispatching the chunks to the engines:

def multi_mcpi(view, nsamples):
    p = len(view.targets)
    if nsamples % p:
        # ensure even divisibility
        nsamples += p - (nsamples%p)

    subsamples = nsamples//p

    ar = view.apply(mcpi, subsamples)
    return sum(ar)/p

%%timeit -n 1
multi_mcpi(dview, int(1e7))

1.71 s ± 30.4 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

Some speedup is seen!

In examples.md:

Mixing Python and R

Your goal now is to define a pandas dataframe, and pass it into an R cell and plot it with an R plotting library.

First you need to install the necessary packages:

!conda install -c r r-essentials
!conda install -y rpy2

To run R from the Python kernel we need to load the rpy2 extension:

%load_ext rpy2.ipython

Run the following code in a code cell and plot it with the basic plot method of pandas dataframes:

import pandas as pd
df = pd.DataFrame({
    'cups_of_coffee': [0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
    'productivity': [2, 5, 6, 8, 9, 8, 0, 1, 0, -1]
})

Now take the following R code, and use the %%R magic command to pass in and plot the pandas dataframe defined above (to find out how, use %%R?):

library(ggplot2)
ggplot(df, aes(x=cups_of_coffee, y=productivity)) + geom_line()

Play around with the flags for height, width, units and resolution to get a good looking graph.

Solution

import pandas as pd
df = pd.DataFrame({
 'cups_of_coffee': [0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
 'productivity': [2, 5, 6, 8, 9, 8, 0, 1, 0, -1]
})

%load_ext rpy2.ipython

%%R -i df -w 6 -h 4 --units cm -r 200
# the first line says 'import df and make default figure size 5 by 5 inches
# with resolution 200. You can change the units to px, cm, etc. as you wish.
library(ggplot2)
ggplot(df, aes(x=cups_of_coffee, y=productivity)) + geom_line();

In examples.md:

Word-count analysis with widgets

This exercise uses the word-count project from earlier lessons.

Have a look under the data/ directory. You will see four .dat files containing word-count statistics from books. You can try opening one.
Open the Launcher, and open a new Text File.

Copy-paste the code below to the text file, and save it to a file zipf.py (note how syntax highlighting gets activated).

def load_word_counts(filename):
    """
    Load a list of (word, count, percentage) tuples from a file where each
    line is of the form "word count percentage". Lines starting with # are
    ignored.
    """
    counts = []
    with open(filename, "r") as input_fd:
    	     for line in input_fd:
          if not line.startswith("#"):
          	   fields = line.split()
                counts.append((fields[0], int(fields[1]), float(fields[2])))
    return counts

def top_n_word(counts, n):
    """
    Given a list of (word, count, percentage) tuples,
    return the top n word counts.
    """
    limited_counts = counts[0:n]
    count_data = [count for (_, count, _) in limited_counts]
    return count_data

def zipf_analysis(input_file, n=10):
    counts = load_word_counts(input_file)
    top_n = top_n_word(counts, n)
    return top_n

Import the new zipf module, and have a look at the docstring for one of the functions:
```
import zipf
zipf.top_n_word?
```

Run the zipf_analysis() function for a processed datafile. Plot the output, and compare with a 1/N function, using the following code:

import matplotlib.pyplot as plt
%matplotlib inline

nmax = 10
z = zipf.zipf_analysis("data/isles.dat", nmax)
n = range(1,nmax+1)
z_norm = [i/z[0] for i in z]
plt.plot(n,z_norm)
inv_n = [1.0/i for i in n]
plt.plot(n, inv_n)

Add an interactive widget to analyze Zipf’s law, using for example this code:

from ipywidgets import interact
import matplotlib.pyplot as plt
%matplotlib inline

nmax = 10
@interact(p=-1.0)
def zipf_plot(p):
    plt.clf()
    n = range(1,nmax+1)
    for f in ["data/isles.dat", "data/last.dat", "data/abyss.dat", "data/sierra.dat"]:
        z = zipf.zipf_analysis(f, nmax)
        z_norm = [i/z[0] for i in z]
        plt.plot(n,z_norm)
    inv_n = [i**p for i in n]
    plt.plot(n, inv_n)

Add another widget parameter nmax to the above code to control the number of words displayed on the x-axis, e.g. nmax=(6,14), and play around with both sliders.

Solution

Code for a widget with sliding bars for both number of words and the inverse power:

from ipywidgets import interact
import matplotlib.pyplot as plt
%matplotlib inline

@interact(nmax=(6,14), p=-1.0)
def zipf_plot(nmax, p):
    plt.clf()
    #plt.figure()
    n = range(1,nmax+1)
    for f in ["data/isles.dat", "data/last.dat", "data/abyss.dat",
              "data/sierra.dat"]:
        z = zipf.zipf_analysis(f, nmax)
        z_norm = [i/z[0] for i in z]
        plt.plot(n,z_norm)
    inv_n = [i**p for i in n]
    plt.plot(n, inv_n)

List of exercises

Summary

Full list

A first computational notebook

Notebooks and version control

Sharing notebooks

Shell commands, magics and widgets

Examples of Jupyter features